Resumen

Este artículo teórico-aplicado tiene como objetivo ilustrar cómo la investigación de operaciones, a través de modelos de programación lineal, puede mejorar la planificación de la producción en una planta afectada por cuellos de botella en varias de sus líneas. La compañía analizada presenta una utilización ineficiente de sus recursos críticos, lo que genera atrasos, sobrecarga en determinadas estaciones de trabajo y una disminución de la capacidad de respuesta ante la variabilidad de la demanda. Ante esta situación, se desarrolla un modelo de programación lineal para la planificación agregada de la producción, considerando capacidades de máquina, disponibilidad de mano de obra, tiempos de proceso y restricciones de demanda por familia de productos. El modelo se formula en notación estándar y se resuelve utilizando los módulos de programación lineal de RStudio, con el fin de comparar facilidad de modelado y calidad de los reportes generados. Los resultados del modelo muestran un incremento en la utilización de los recursos críticos y una reducción de los cuellos de botella en las principales líneas de producción, al redistribuir las cargas de trabajo entre máquinas y periodos.

La solución óptima permite aumentar el volumen producido en las familias con mayor contribución marginal, respetando las restricciones de capacidad y demanda, lo que se traduce en una mejora significativa de las ganancias esperadas y en una mayor estabilidad del plan de producción. A modo de conclusión, se discuten las ventajas y limitaciones de aplicar programación lineal en entornos reales de manufactura, así como las implicaciones para la toma de decisiones en planificación de la producción. El lector podrá comprender el uso básico de estas herramientas de optimización y la empresa contará con un referente cuantitativo para rediseñar su sistema productivo y sus políticas de planificación.

Palabras clave: Asignación de recursos; cuellos de botella; ganancias; investigación de operaciones; mejora de procesos

Abstract

This theoretical-applied article aims to illustrate how operations research, through linear programming models, can improve production planning in a plant affected by bottlenecks in several of its lines. The analyzed company shows inefficient utilization of its critical resources, which generates delays, overload at certain workstations, and a reduction in its ability to respond to demand variability. In response to this situation, a linear programming model for aggregate production planning is developed, considering machine capacities, labor availability, processing times, and demand constraints by product family. The model is formulated in standard notation and solved using the linear programming modules of RStudio, to compare ease of modeling and quality of the generated reports. The results of the model show an increase in the utilization of critical resources and a reduction of bottlenecks in the main production lines by redistributing workloads across machines and periods.

The optimal solution allows an increase in the volume produced in families with the highest marginal contribution, while satisfying capacity and demand constraints, which translates into a significant improvement in expected profits and greater stability of the production plan. In conclusion, the advantages and limitations of applying linear programming in real manufacturing environments are discussed, as well as the implications for decision-making in production planning. The reader will be able to understand the basic use of these optimization tools, and the company will have quantitative reference to redesign its production system and planning policies.

Keywords: Bottlenecks; operations research; process improvement; production gains; resource allocation

Resumo

Este artigo teórico-aplicado tem como objetivo ilustrar como a pesquisa operacional, por meio de modelos de programação linear, pode melhorar o planejamento da produção em uma planta afetada por gargalos em várias de suas linhas. A empresa analisada apresenta utilização ineficiente de seus recursos críticos, o que gera atrasos, sobrecarga em determinados postos de trabalho e redução de sua capacidade de responder à variabilidade da demanda. Diante dessa situação, desenvolve-se um modelo de programação linear para o planejamento agregado da produção, considerando as capacidades das máquinas, a disponibilidade de mão de obra, os tempos de processamento e as restrições de demanda por família de produtos.

O modelo é formulado em notação padrão e resolvido utilizando os módulos de programação linear do RStudio, com o objetivo de comparar a facilidade de modelagem e a qualidade dos relatórios gerados. Os resultados do modelo mostram um aumento na utilização dos recursos críticos e uma redução dos gargalos nas principais linhas de produção, por meio da redistribuição das cargas de trabalho entre máquinas e períodos.

A solução ótima permite aumentar o volume produzido nas famílias com maior contribuição marginal, ao mesmo tempo em que satisfaz as restrições de capacidade e demanda, o que se traduz em uma melhoria significativa nos lucros esperados e em maior estabilidade do plano de produção. Conclui-se discutindo as vantagens e limitações da aplicação da programação linear em ambientes industriais reais, bem como suas implicações para a tomada de decisão no planejamento da produção. O leitor poderá compreender o uso básico dessas ferramentas de otimização, e a empresa disporá de uma referência quantitativa para redesenhar seu sistema produtivo e suas políticas de planejamento.

Palavras-chave: alocação de recursos; ganhos de produção; gargalos; melhoria de processos; pesquisa operacional.

Introducción

En el contexto actual, la industria de productos semiconductores se caracteriza por un incremento constante en la demanda, alta variabilidad en los procesos y la necesidad de mejorar la eficiencia operativa y la planificación efectiva de las líneas de producción lo que es fundamental para mantener la competitividad empresarial. La asignación óptima de recursos, la sincronización de actividades y la minimización de los tiempos de producción son aspectos claves que impactan directamente en el desempeño global de las organizaciones manufactureras.

La empresa utilizada para la aplicación de este caso, se dedica a la fabricación de componentes electrónicos. Esta enfrenta estos retos significativamente relevantes en la gestión de sus procesos productivos, especialmente en la planificación de sus líneas de producción. Ante esta problemática, se plantea la implementación de herramientas cuantitativas basadas en modelos matemáticos robustos y replicables, que fortalezcan la toma de decisiones operativas.

Marco teórico

La aproximación a un marco conceptual constituye un paso fundamental en el proceso de una investigación tanto científica como académica. Consiste en una revisión sistemática o crítica de una lectura existente con relación al tema de estudio, esta proporciona una base conceptual sólida que ayuda con el desarrollo de la investigación. 

Algunos conceptos relevantes en esta rama de investigación son:

Los cuellos de botella en los procesos de producción representan puntos de estrangulamiento (zonas críticas donde el rendimiento global se ve condicionado, sin importar cuán eficiente sea el resto de la línea). Que limitan el rendimiento global y la eficiencia de la línea productiva.  La metodología de atenuación de los cuellos de botella se apoya en dos métodos diferenciados, el primero, el método de detección anticipativo y el segundo, en el Modelo de expansión de los cuellos de botella. (Lastra, 2016).

En 1987, Morshedi y Tapia demostraron que el algoritmo de Karmarkar (1984) para programación lineal se puede deducir de una formulación especial del método del gradiente para programación no-lineal.   En efecto, como se presenta en Martínez (1990), el algorítmo de Karmarkar es equivalente al método del gradiente aplicado al problema de programación no lineal que resulta cuando el problema de programación lineal (Martinez,1991). 

En el ámbito industrial y de gestión, estas herramientas se vuelven increíblemente valiosa para identificar causas de problemas, evaluar mejoras implementadas y planear acciones basadas en evidencia histórica. “El diseño de investigación implicó el análisis de documentos históricos, que proporcionan información sobre organizaciones, individuos y eventos de épocas anteriores” (Pacheco & Alfaro, 2023)

Las capacidades tecnológicas de una organización son un factor clave que determinan su ventaja competitiva en el mercado. No se trata únicamente de recursos disponibles, sino de un conjunto de competencias que permiten innovar, adaptarse y sostener ventajas frente a la competencia. Según Barcenilla y Lozano (2000), estas capacidades actúan como un determinante fundamental de la ventaja absoluta, resaltando que, a largo plazo, es precisamente esta ventaja la que influye en la evolución del comercio internacional.

Los modelos de simulación son herramientas que permiten replicar el comportamiento de sistemas reales con el fin de analizar, entender y predecir su funcionamiento bajo diferentes condiciones. Su utilidad se extiende desde la comprensión de procesos complejos hasta la evaluación de alternativas de mejora que serían costosas o inviables de ensayar directamente en la práctica. 

En general, el problema de validar modelos de simulación es un tanto complejo, ya que lleva consigo un sinnúmero de situaciones de tipo práctico, teórico, estadístico e inclusive filosófico; sin embargo, se recomienda tener en cuenta: 

1. Qué tanto coinciden los datos simulados con los datos históricos 

2. Qué tanto se parecen las predicciones del comportamiento del sistema real realizadas con los datos simulados, y las realizadas con los datos muestrales del sistema real, en un momento dado (Burbano et al., 2014) 

El análisis de los procesos productivos en las organizaciones revela que la variabilidad, la capacidad tecnológica y la gestión eficiente de los recursos son factores clave que determinan la competitividad y mejora continua en una empresa. La variabilidad en los procesos de producción, especialmente en contextos donde se manejan diferentes familias de productos, genera desafíos significativos, como los cuellos de botella, que limitan la eficiencia global y aumentan los costos operativos. 

Materiales y métodos

Esta investigación es de tipo explicativa, debido a que surge de la necesidad de comprender y mejorar el balance actual de las líneas de producción de la compañía, identificando las relaciones causa-efecto entre diferentes variables operativas. El enfoque es mixto secuencial, ya que representa una integración sistemática de los métodos cuantitativo y cualitativo en un solo estudio, en este caso los componentes se ejecutan en fases sucesivas.

En este caso, la recopilación de datos se obtuvo directamente de la empresa, por medio de evaluaciones en siete áreas diferentes, estas evaluaciones constan de tiempos promedio de operación y la variabilidad en los mismos por la diferencia en los productos, una vez registrada la información, la siguiente fase es crear un caso para programación lineal determinando una función objetivo y restricciones, luego de esto se plantea el problema en la aplicación seleccionada, la cual, es RStudio y esta dará el resultado ideal de lo que se debe fabricar según lo planteado. 

La metodología se basa en el desarrollo de un modelo de programación lineal orientado a optimizar la planificación de las líneas de producción de componentes electrónicos semiconductores. Se adopta un enfoque aplicado, utilizando datos reales de la planta relacionados con capacidades de máquina, tiempos de proceso, disponibilidad de mano de obra y demanda por familia de productos. El objetivo metodológico central es formular un modelo matemático que represente fielmente las restricciones operativas clave y permita evaluar distintos escenarios de producción.

Resultados

Con el gráfico 1, se observa la variabilidad de tiempo existente en los procesos por los que deben pasar los productos, esto debido a que en el 90% de las áreas las operaciones son manuales por eso, hay consumo excesivo de tiempo.

La primera área es la más pesada ya que consiste en 17 subprocesos delicados y manuales, en la evaluación final se determina si el producto pasa o no a la siguiente fase, y un 30% del tiempo se debe rehacer todo nuevamente, el área de menor tiempo es la última ya que es empaque, y aunque igual es manual, ya el producto por estar hecho se guarda con cuidado pero es más rápido, sin embargo, no tan eficientemente rápido como debería.

Gráfico1.

Tiempo promedio en horas del producto en cada área

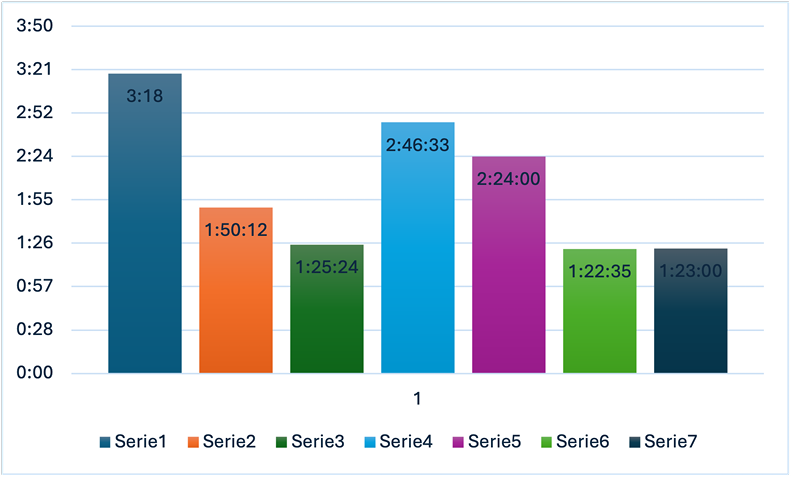
Nota. Elaboración propia.

Desarrollo de la propuesta

La planta de la empresa que permitió este caso se localiza en Alajuela, Costa Rica y presenta un serio problema de cuellos de botella en algunas áreas, lo cual, provoca retrasos en los pedidos de los clientes y pérdidas de dinero masivas debido a que el trabajo es bajo pedido y los procesos son delicados y manuales en un 90% lo que incide directamente con la planificación, ya que esta, en lugar de establecerse en una fecha fija, pasa en constante cambio, que no es lo ideal. 

Se cuenta con 3 familias de productos que requieren mayor tiempo en producción y al mismo tiempo son los de mayor demanda:

Familia 1= Productos TVA, Familia 2= Productos TS, Familia 3= Productos H.

Al ser los que más solicitan los clientes, se requiere de una minimización del tiempo de producción para cumplir con la mayoría los pedidos antes del 1ro de diciembre, cubrir el 95% de esta demanda con el fin de iniciar el año siguiente sin deudas con los clientes, y poder iniciar fresco el año 2026, cumpliendo ahora puntualmente con todo.

Modelo teórico aplicado

Función objetivo

$\text{min}{\sum }_i{\text{Tiempo\_produccion}}_i\times x_i+\text{Costos\_inversion}\left(y_A\right)$

Restricciones

1. Cobertura del 95% de la demanda para cada familia:

${\sum }_{i\in {\text{Familia}}_j}{x}_i\ge 0.95\times {\text{Demanda}}_j,\forall j=1,2,3$

2. Diferencia de 8.5 horas en área láser entre Familia 1 y Familia 3 (más tiempo para Familia 1):

$$\begin{gathered} {\text{Tiempo\_Laser\_Familia1}}_{}=9\times {\sum }_{i\in \text{Familia1}}{x}_i \\ {\text{Tiempo\_Laser\_Familia3}}_{}=0.5\times {\sum }_{i\in \text{Familia3}}{x}_i \\ \text{Tiempo\_Laser\_Familia1}=\text{Tiempo\_Laser\_Familia3}+8.5\times y_B \end{gathered}$$

La variable  indica si se aplicó especialización para Thin Film (opción B), esto puede modificar la diferencia de tiempo.

3. Tiempo adicional para Familia 3 en área Thin Film (1.5 horas más por unidad):

$\text{Tiempo\_ThinFilm\_Familia3}=\left(\text{Tiempo\_estandar}+1.5\right)\times {\sum }_{i\in \text{Familia3}}{x}_i$

La especialización del personal (opción B, $y_B$ ) puede reducir este tiempo.

4. Fallos en área Product Display para Familia 2 (35%):

$x_i\ge \left(\frac{{\text{Demanda}}_i}{1-0.35}\right),\forall i\in \text{Familia2}$

Para compensar las pérdidas por fallas,

La opción C (mezclas específicas) puede reducir este efecto, modelado con $y_C$ .

5. Fallos en área Visual para Familia 1 (65%):

$x_i\ge \left(\frac{{\text{Demanda}}_i}{1-0.65}\right),\forall i\in \text{Familia1}$

La rotación de personal (opción D, $y_D$ ) puede mejorar la tasa efectiva, ajustando la falla.

6. Minimización del tiempo total de producción:

La función objetivo considera:

$\text{min}{\sum }_i{\text{Tiempo\_produccion}}_i\times x_i+\text{Costos\_inversion}\left(y_A\right)$

Modelo final:

$\text{min}{\sum }_i{\text{Tiempo\_produccion}}_i\times x_i+\text{Costos\_inversion}\left(y_A\right)$

${\sum }_{i\in \text{Familia}j}{x}_i\ge 0.95\times {\text{Demanda}}_j,\forall j=1,2,3$

$$\begin{gathered} \text{Tiempo\_Laser\_Familia1}=9\times {\sum }_{i\in \text{Familia1}}{x}_i \\ \text{Tiempo\_Laser\_Familia3}=0.5\times {\sum }_{i\in \text{Familia3}}{x}_i \\ \text{Tiempo\_Laser\_Familia1}=\text{Tiempo\_Laser\_Familia3}+8.5\times y_B \end{gathered}$$

$\text{Tiempo\_ThinFilm\_Familia3}=\left(\text{Tiempo\_estandar}+1.5\right)\times {\sum }_{i\in \text{Familia3}}{x}_i$

$$\begin{gathered} x_i\ge \left(\frac{{\text{Demanda}}_i}{1-0.35}\right),\forall i\in \text{Familia2} \\ {x}_i\ge \left(\frac{{\text{Demanda}}_i}{1-0.65}\right),\forall i\in \text{Familia1} \end{gathered}$$

Solución con RStudio:

> # Resolver el problema (minimización)

> resultado <- lp(“min”,

+ f.obj,

+ f.con,

+ f.dir,

+ rhs,

+ binary.vec = 4:7,

+ all.int = TRUE)

> print(resultado$status) # 0 es solución óptima

[1] 0

> print(resultado$objval)

[1] 108449.5

> print(resultado$solution)

[1] 333 5977 570 0 1 0 0

Análisis de la solución

Según los resultados obtenidos con R Studio, la cantidad que se debería producir en este tiempo, si se quiere cubrir la demanda al 95% al 1ro de diciembre es:

Familia 1: 333 unidades, Familia 2: 5977 unidades, Familia 3: 570 unidades, generando una ganancia de $108 499.

Basado en los resultados obtenidos, se deberían fabricar 6880 unidades mensualmente sumando todos los productos, de las tres familias, para que se logre cumplir con la meta y más importante con los clientes. Además, con este nivel de producción propuesto se presenta una mejoría en ganancias, y un mayor nivel de confidencialidad por parte de la clientela.

Con el modelo aplicado, conociendo la cantidad que se debe producir, y si teóricamente se logra cumplir con la meta dada por la aplicación, las ganancias aumentarían a un 69%.

Conclusiones

La propuesta teórica de producir un total de 6,880 unidades mensuales, distribuidas en las tres familias de productos, da el resultado necesitado de cumplir con la demanda al 95%, mejorando el nivel de satisfacción de los clientes, asegurando la continuidad del negocio.

Con la implementación del modelo con la aplicación R Studio, se muestra la cantidad exacta de producción necesaria para obtener un incremento significativo en las ganancias, no solo porque el método lo dice en los resultados, sino porque al comparar las finanzas si es evidente el cambio.

El modelo facilitó la toma de decisiones en el enfoque de mejorar la eficiencia operativa, ya que mostró de forma clara la comparación entre la expectativa y la realidad tanto productiva como financieramente.

Aplicar las técnicas cuantitativas de optimización no solo influye en el área financiera, sino que también en los clientes incrementando su confianza y satisfacción.

Referencias

Aguirre Pozo, C. G. (2017). Análisis situacional de control de la eficiencia operativa de una empresa. RECIMUNDO: Revista Científica de la Investigación y el Conocimiento, 1(4), 266–279.

Arce-Villalobos, K., Arias-Castro, A., González-Jiménez, Y., Hernández-Ugalde, K., & Mora-Barrantes, J. C. (2021). Evaluación del impacto ambiental de una planta de lácteos en Costa Rica. Revista Tecnología en Marcha, 34(3), 83–95. https://doi.org/10.18845/tm.v34i3.4919

Ballesteros Riveros, D. P., & Ballesteros Silva, P. P. (2004). La Logística Competitiva y la administración de la cadena de suministros. Scientia et Technica, 1(24), 201–206.

Berrones-Sanz, L. D., González-Peña, E. C., Lámbarry Vilchis, F., & Rocha Lona, L. (2020). Estudio de los efectos de las condiciones laborales de los conductores de autotransporte en la cadena de suministro en México. Dirección y Organización, 87–98. https://doi.org/10.37610/dyo.v0i71.580

Blanco Obando, E. (2019). Reconversión productiva y condiciones de vida de la población rural en Costa Rica, 1990-2018. Revista de Ciencias Sociales, 165, 15–27.

Campos Quispe, L. F. (2020). Diseño e implementación de una interface usuario-máquina basada en visión computacional para automatizar la selección de frutos cítricos según la forma, tamaño, color y defectos externos [Tesis de magíster, Pontificia Universidad Católica del Perú]. https://tesis.pucp.edu.pe/server/api/core/bitstreams/aef12673-59de-4058-9b8a-89a1b09b50db/content

Cardoso Espinosa, É. O. (2023). Student assessment of their mathematical education in a postgraduate course in administration. Apertura, 15(2), 36–53. https://doi.org/10.32870/Ap.v15n2.2413

Castellón Zelaya, L. A. (2018). Análisis del proceso de medición de cargas de trabajo en el Instituto Nacional de aprendizaje –INA- Costa Rica. InterSedes, 18(38). https://doi.org/10.15517/isucr.v18i38.32671

Espinoza Ramirez, J. L. (2019). Análisis, diagnóstico y propuesta de mejora en la línea de ensamble del proceso de producción de grupos electrógenos utilizando las herramientas de la metodología TLS (Teoría de las restricciones “TOC” – Lean Manufacturing – Six Sigma). http://hdl.handle.net/20.500.12404/13290

Medina Chacón, E., & Illada García, R. (2015). Heurística para el balance de líneas de ensamble con consideraciones ergonómicas. Ingeniería Industrial, 14(1), 23–35.

Mendoza, M. (1994). Técnicas de observación directa para estudiar interacciones sociales infantiles entre los Toba. Runa: archivo para las ciencias del hombre, 21(1), 241–262.

Oldenburg Basgal, D. M. (2008). Gerencia de proyectos. Visión de futuro, 10(2), 175–191.

Orozco-Crespo, E., Sablón-Cossío, N., Rodríguez-Sánchez, Y., González-Garzón, J. C., & Sánchez-Galván, F. (2021). Secuenciación de operaciones por simulación en la empresa Puntadas, S.G. Revista Tecnología en Marcha. https://doi.org/10.18845/tm.v34i1.4823

Ortiz Porras, J. E. (2022). Modelo de gestión para la aplicación de herramientas Lean Manufacturing para la mejora de la productividad en una empresa de confección de ropa antiflama de Lima – Perú [Universidad Nacional Mayor de San Marcos]. hhttps://hdl.handle.net/20.500.12672/17736

Ramírez Peña, M. (2021). Análisis de la sostenibilidad de la cadena de suministro de la construcción naval en su adaptación a la industria 4.0 [tesis doctoral, Universidad de Cádiz]. https://dialnet.unirioja.es/servlet/tesis?codigo=303285

Robles, E. A. (2021). Crecimiento de la productividad total de los factores en Costa Rica e inestabilidad macroeconómica. Revista de Ciencias Económicas, 39(1), 1–24. https://doi.org/10.15517/rce.v39i1.47622

Salas, S. D., Mena, D. R., & Domínguez, C. R. (2023). Guía para la elaboración de trabajos fin de grado y trabajos fin de máster en psicología y ciencias afines. Volumen 2. Dykinson. https://dialnet.unirioja.es/servlet/libro?codigo=940998

Nuestros artículos son publicados bajo los términos de la licencia internacional Creative Commons Atribucion-NoComercial-CompartirIgual 4.0.